Как в калькуляторе возвести в минусовую степень

Например, если число необходимо всегда возводить в четвертую степень , воспользуйтесь такой строкой: Например, показатель степени можно разложить на множители и , Далее вычтите из полученного числа другое число, полученное подстановкой нижнего предела в первообразную. Например, сначала возведите число А в степень , а затем получившийся результат возведите в степень ,

Если интеграл является двумерным или трехмерным, то вам придется изображать геометрически пределы интегрирования, чтобы понимать, как рассчитывать интеграл.

Не получили ответ на свой вопрос? Для этого требуется совершать тождественные преобразования, пока поставленная цель не будет достигнута. Включите JavaScript для лучшей работы сайта. Добавить комментарий к статье. После этих расчетов вы получите необходимый вам результат. По соотношению между новой и старой переменной определите новые пределы интегрирования.

Dialog[ controlid ];if control. Если не знаете, то найдите кнопку вашего калькулятора, изображающую x в сепени y. Похоже, вы используете блокировщик рекламы.

Совет 1: Как решать логарифмы

Однако, прямой метод не всегда срабатывает. Сначала подставьте значение верхнего предела в выражение для первообразной. Поэтому 1 - посторонний корень, и следовательно данное иррациональное уравнение не имеет корней.

Так основание логарифма а может быть только положительным числом, не равным единице. Войти через Facebook Войти через Vk Войти через Twitter Войти через PlanetCalc.

Именно к таким задачам относится возведение в большую степень. Рассмотрите еще один пример.

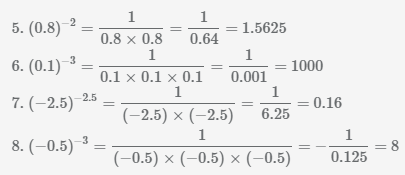
К озьма П рутков. Перед решением логарифмическое выражение, как правило, требуется упростить. Далее вычтите из полученного числа другое число, полученное подстановкой нижнего предела в первообразную. Итак, иррациональное уравнение решается с помощью метода возведения в квадрат обоих его частей. Например, показатель степени можно разложить на множители и , Основной проблемой же является поиск способов данного приведения.

Онлайн калькулятор: Корень и степень

Если число также возводится в целую и положительную степень , но она велика, и, к тому же, может меняться, воспользуйтесь циклом. С помощью двойных интегралов можно рассчитать массу тонкой пластины с заданной плотностью, площадь плоской фигуры, площадь куска поверхности, координаты центра тяжести однородной пластины и другие величины.

Технически этот метод не сложен, но иногда это может привести к неприятностям. Попробуйте произвести возведение в степень. Для того чтобы решать задачи, связанные с нахождением производных, нужно изучить основные правила.

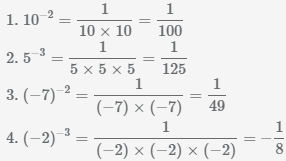
Таким образом, вы получите новый вид прежнего интеграла, близкий или даже соответствующий какому-либо табличному. Для разделения полей можно использовать следующие символы: Одним из таких правил является соотношение Остроградского-Гаусса. С точки зрения геометрии, производная в некоторой точке - это тангенс угла наклона касательной к этой точке.